Черепаха наносит ответный удар - 2

Ну, а теперь - ответ на задачку про черепаху и Ахиллеса. И ответ этот, как многие догадались (или рассчитали) - да, черепаха сможет догнать Ахиллеса. Более того, она сможет его догнать, даже если скорости будут различаться не в два раза, а в 10, в 100... да вообще в произвольное число раз.

Собственно, как это вообще возможно - легко понять и без точных расчетов, на уровне простой логики. Представим, что черепаха неподвижно замерла в некоей точке пути, а Ахиллес продолжает панически от нее уплётывать. Так как резиновая лента растягивается равномерно, то отношение A:B (отношение длины резиновой ленты, которую осталось преодолеть черепахе - к полной длине ленты) будет оставаться неизменным: отрезок впереди растет в той же самой мере, что и длина всей ленты. А вот если черепаха будет двигаться - то отношение это, мало-помалу, будет уменьшаться, пока наконец не достигнет нуля.

Т.е. - черепаха обязательно настигнет Ахиллеса.



Можно проделать и точные расчеты - составить уравнение движения (его чуть проще вывести, если предположить, что длина ленты остается неизменной - но, вместо этого, уменьшаются размеры и, соответственно, скорость черепахи), а потом его решить (уравнение будет интегральным, но очень простым, так что решить его не представит ни малейшей проблемы). Конечная же формула будет такой:



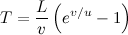
где L - начальное расстояние между Ахиллесом и черепахой, v - скорость Ахиллеса, u - скорость черепахи.

Таким образом, для наших начальных условий (L = 100 метров, v = 5 м/с, u = 2.5 м/с) мы получаем, что черепаха сможет свершить свое справедливое возмездие всего примерно через две с половиной минуты.

Однако, как видно из формулы, время зависит от соотношения скоростей экспоненциальным образом, так что при разнице скоростей в десять раз (скорость черепахи более близка к привычно-"черепашьим" 0.5 м/с) погоня займет более пяти суток. Если же мы замедлим черепаху еще в пять раз - то до момента сладостной мести черепахе (и Ахиллесу, и Земле тоже) дожить будет уже не суждено - время погони значительно (в сто тысяч раз с гаком) превысит возраст нашей Вселенной.

Именно поэтому так важен каждый голос на выборах. :)

И, раз уж была упомянута Вселенная - на самом деле, эта задачка имеет прямое к ней отношение. Ведь, как это усиленно подчеркивается во всех книгах и лекциях по космологии, расширение Вселенной - это не разлет галактик _в_ пространстве, это "разлет" самого пространства-времени, почти полный аналог растяжения резиновой ленты в нашей шутливой задачке. И именно поэтому, в равномерно расширяющейся Вселенной, хотя скорость удаления далекой галактики может в произвольное число раз превышать скорость света - тем не менее световой луч, пущенный к этой галактике, _сможет_ ее достигнуть, пусть и за чудовищно большой промежуток времени.

В самом деле, скорость удаления галактики за счет космологического расширения можно получить из закона Хаббла: v = H*r, где H - постоянная Хаббла, современные оценки на величину которой составляют примерно 70 (км/с)/Мпк, r - расстояние до галактики в мегапарсеках. То есть галактики, удаленные от нас на 4 с лишним гигапарсека и более - удаляются со скоростью, превышающей скорость света.

Далее, квадрат интервала для плоской фридмановской модели Вселенной задается следующей формулой:



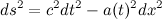
где a(t) - масштабный фактор Вселенной, описывающий изменение со временем расстояний в ней за счет космологического расширения.

Для света, как известно, квадрат интервала равен нулю - что позволяет легко составить уравнение, которое связывает расстояние r, которое нужно пройти свету - и время T, которое потребуется ему на это:



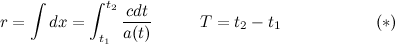
В равномерно расширяющейся Вселенной:



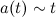
И легко получаем:



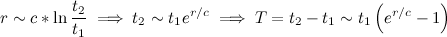
А так как по закону Хаббла расстояние r линейно связано со скоростью удаления v - то получаем практически полный аналог уравнения "Ахиллеса и черепахи".

Однако следует сделать важное уточнение: мы рассматривали _гипотетический_ случай равномерного расширения Вселенной. В нашей же реальной Вселенной - ситуация еще интереснее. У нее были периоды, когда она расширялась с замедлением (на радиационно-доминированной стадии эволюции Вселенной масштабный фактор был пропорционален корню из времени, на материально-доминированной - времени в степени две трети), т.е. задача для черепахи света была еще проще.

Но несколько миллиардов лет (около 7, если точнее) она перешла на расширение ускоренное, что обусловлено наличием в ней так называемой темной энергии. И вот сейчас Ахиллес действительно может сбежать от черепахи существуют галактики, которых ни наш свет, ни, тем более, наши космические корабли не достигнут уже никогда. Собственно, в этом своем постинге я давал ссылку на расчеты моего коллеги по данному вопросу.

И ходя для их повторения требуется совместное решение уравнений Фридмана и уравнений состояний всех компонент Вселенной (излучения, обычного и темного вещества, темной энергии), на качественном уровне к подобному результату легко можно прийти, рассмотрев предельный случай - когда во Вселенной нет ничего, кроме темной энергии (в форме космологической постоянной), так что масштабный фактор увеличивается по экспоненциальному закону:



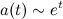
Решив при таком условии уравнение (*) - можно легко увидеть, как возникает космологический горизонт событий, который на самом деле во многом похож по своим свойствам на горизонт событий черных дыр.

Впрочем, это уже - совсем другая история.