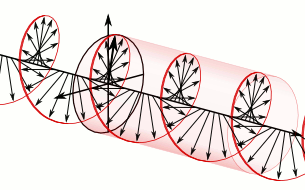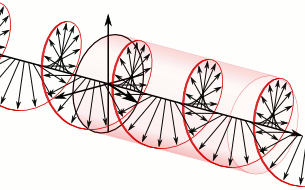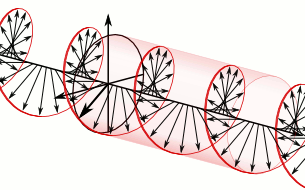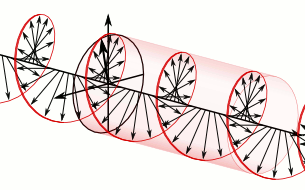
В продолжение темы про фотоны с орбитальным угловым моментом (ОУМ) — вот чуть более технический пост про то, как орбитальный угловой момент уживается с поляризацией.Орбитальный угловой момент и поляризацияПрежде всего, я еще раз хочу подчеркнуть: та «закрученность», которая есть у светового луча с орбитальным угловым моментом — это не круговая поляризация, это совсем другая характеристика. Бывает ОУМ без круговой поляризации, бывает круговая поляризация без ОУМ, бывает и то, и другое вместе. Это две разные характеристики светового поля.Есть знаменитая такая картинка, на которой световая волна изображена этакой крутящейся спиралью:
Она похожа на ту, что я приводил в прошлом посте.
Но надо понимать, что на верхней картинке изображено вовсе не распределение электрического поля в реальном пространстве, а лишь условно показан вектор этого поля вдоль оси движения волны. Эта картинка не меняется при смещении в поперечном направлении, поскольку в плоской волне никакой зависимости полей от поперечных координат нет. Т.е. реально такая волна (если бы мы рисовали именно фазу волны, а не вектор электрического поля) бежит просто вперед, одна плоскость за другой.А вот на картинке с закрученной волной (скалярной волной, т.е. волной не имеющей никакой поляризации) винтовая поверхность — это поверхность постоянной фазы в реальном пространстве. Такая волна действительно бежит вперед, одновременно накручиваясь вокруг оси.Разделение спина и ОУМНа самом деле, во всей этой истории с фотонами, несущими орбитальный угловой момент, есть один сложный и глубокий вопрос — в какой степени можно вообще разделять полный угловой момент фотона на орбитальную и спиновую часть. Спин (т.е. поляризация) и орбитальный момент — это две разновидности полного момента импульса. В квантовой механике эти две величины описываются своими операторами:
и
, а оператор полного спина есть просто их сумма
. В квантовой механике по построению понятно, что есть ОУМ и что есть спин, поэтому вопросов об их разделении не возникает.В теории поля (даже не-квантовой) всё хитрее. Там мы вводим многокомпонентное поле и изучаем, как оно преобразуется при переходе к другой системе координат или системе отсчета. Из этого рассмотрения само вытекает понятие сохраняющего углового момента и понятие спина. Полный момент импульса J (а точнее, его плотность) для электромагнитного поля легко записывается через электрическое и магнитное поля:
. Эта величина калибровочно-инвариантна и потому наблюдаема.Однако в квантовой теории разделить ее на два векторных оператора, орбитальный и спиновый, которые обладали бы правильными коммутационными свойствами и были бы еще калибровочно-инвариантными, не удается. Поэтому возникает впечатление, что разделение полного момента импульса на две части для этих частиц нефизично. Разделение спина и ОУМ в сильных взаимодействияхЭта проблема еще больше усугубляется в физике элементарных частиц, когда мы вместо электромагнитных взаимодействий рассматриваем сильные взаимодействия (вместо фотонов — глюоны, вместо электронов — кварки). Теория сильных взаимодействий неабелева и потому нелинейна; в ней отделить свойства кварков от свойств глюонов еще тяжелее. Поэтому тут вопрос о том, можно ли разумным образом ввести орбитальный угловой момент кварков и глюонов встает в полный рост.
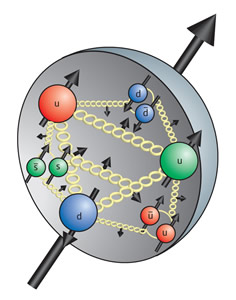
Из чего складывается спин быстро движущегося протона? Кто главнее: спин кварков, спин глюонов, их орбитальный угловой момент, или же это разделение вообще не очень осмысленно?И это не праздный интерес. Дело в том, что уже давно известно, что спин быстро летящего поляризованного протона вовсе не складывается из одних лишь спинов кварков (это так называемая «загадка спина протона», краткий обзор нынешней ситуации см. в arXiv:0905.4619). На самом деле поляризация кварков дает совсем небольшой вклад, и значит, почти весь спин протона берется откуда-то еще. На наивном языке обычно приговаривают, что есть мол еще спин глюонов, а также орбитальный момент кварков и глюонов — и всё это должно вместе давать полный спин протона. Сейчас ведутся даже эксперименты, которые пытаются узнать, какой вклад вносят эти компоненты момента импульса в полный спин протона, а тут оказывается, теоретики спорят о том, как вообще определять эти вещи.Над этой проблемой люди бьются вот уже десяток лет. Почувствуйте ситуацию: тут сложности не в том, как с помощью теории описать экспериментальные явления, а в том, как вообще правильно обращаться с теорией. Желающим посмотреть, что там за баталии, рекомендую недавнюю статью Эллиота Лидера arXiv:1101.5956; там есть сначала подробное обсуждение электродинамики, а затем сильных взаимодействий, и ссылки на разные предыдущие работы.Так разделяются или нет?Вернемся снова к фотонам. Что сейчас известно точно? Во-первых, под разделением спина и ОУМ можно подразумевать разные вещи. Это может быть сильное утверждение о разделении операторов как векторов, может быть более слабое утверждение о разделении только z-компонент операторов (т.е. спиральностей), а может быть и еще более слабое утверждение об осмысленном разделении средних значений этих операторов по тем или иным состояниям фотонов.Во-вторых, если говорить про самое слабое утверждение, то в параксиальном приближении (т.е. световая волна очень плавно меняется в поперечной плоскости) оно работает. Доказывается это несложно. Мы пишем вектор-потенциал с закрученным профилем (с числом закрутки m) и считаем, что у него есть только одна компонента (например, по оси x), что отвечает линейной поляризации. Считаем плотность полного момента импульса (а он определен однозначно), делим его на плотность потока и получаем m/ω. На квантовом языке это означает, что каждый фотон несет m квантов полного углового момента.Теперь запишем двухкомпонентный вектор-потенциал, причем его комплексные x и y компоненты сдвинуты по фазе на π/2 — это как раз отвечает круговой поляризации. Повторяем расчет и получаем (m+1)/ω для положительной спиральности и (m−1)/ω — для отрицательной. Т.е. спиновой и орбитальный вклад в средние значения момента импульса мило уживаются друг с другом.А что будет, если выйти за пределы параксиального приближения? Если повторить те же расчеты, то окажется, что спин и ОУМ так просто не суммируются. Однако на эту ситуацию можно посмотреть еще и вот так: в непараксиальном закрученном свете наводится спин-орбитальное взаимодействие (и это в линейной волне!), которое и мешает этому разделению. Такую точку зрения предлагает Константин Блиох в статье arXiv:1006.3876 (и вот еще появившаяся на днях статья arXiv:1105.0331, где он то же описание разрабатывает для релятивистских закрученных электронов). На всякий случай скажу, что сомнений в том, можно ли экспериментально получать световые пучки, комбинирующие орбитальную закрученность с поляризацией, не возникает — конечно, можно. Вопрос только в том, как правильно такие состояния описывать.Экзотические поляризационные состоянияНапоследок, есть очень наглядное объяснение, почему непараксиальный случай вообще намного сложнее параксиального, когда дело касается поляризации. В строгой плоской волне электрическое и магнитное поле лежат в плоскости, перпендикулярной направлению движения волны. Для не-плоской волны такой единой плоскости нет. В результате в какой-то выбранной точке вектор электрического поля может иметь все три компоненты. Конечно, локально этот вектор по-прежнему лежит в плоскости, ортогональной локальному направлению движения волны, но проблема в том, что эти плоскости разные для разных точек пространства.Такая ситуация называется трехмерный свет. Описание такого поля поляризаций, которое меняется от точки к точке — отдельная интересная тема в оптике. Там есть разные поляризационные сингулярности и нетривиальные топологические штуки. Я как-то рассказывал про них в своем блоге и в новости Поляризация света может закручиваться наподобие ленты Мёбиуса.
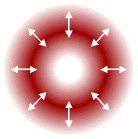
Радиально поляризованный свет:вектор электрического поля направлен вдоль радиус-вектора.В параксиальном приближении ситуация резко упрощается. Мы пренебрегаем z-компонентами полей, и фактически считаем, что все они лежат в единой плоскости. Это конечно резко упрощает описание, но при этом мы теряем некоторые богатства общего трехмерного света. Тем не менее, даже в этой упрощенной ситуации существуют необычные поляризационные состояния света — например, радиальная поляризация, показанная на рисунке выше.
Комментарии (0)