Как я помог мировому заговору нефтяных компаний против источников дешевой энергии

Я давно угрожал некоторым людям прочитать персональную лекцию про каналирование, и чтобы объяснения не пропали втуне, сделал ее в виде поста. Остальным читателям под кат можно не лезть, для вас я добавил в конец историю про прожект кристаллического термоядерного реактора на встречных пучках с полным его разоблачением.
Каналирование — это явление, состоящее в том, что быстрые положительно зараженные частицы, влетев в кристалл, вдоль некоторых направлений в нем могут пролететь на гораздо большее расстояние, не останавливаясь, чем обычно в среде. Причину проще показать, чем рассказать словами:
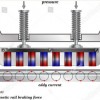
Синие шарики изображают атомы, организованные в кристаллическую решетку (такую картину можно увидеть увеличив срез кристалла кремния в несколько десятков миллионов раз) . В кристалл влетает быстрая положительно заряженная частица, например протон (далее мы будем называть ее ионом). Если она влетела почти параллельно цепочкам атомов, то отталкивание от положительно заряженных ядер атомов будет работать как стенки трубы (отсюда и термин «каналирование» - Ваш К.О.) . При этом траектория иона будет выглядеть как зеленая кривая на рисунке. Поскольку ион не приближается к атомам, потери энергии на единицу длины пути у него будут относительно невелики. Если же ион влетел под большим углом, то поле ядер не может остановить его поперечное движение, его типичная траектория в этом случае показана красной (почти)прямой. Собственно, именно так обычно движутся частицы в среде — сталкиваясь с атомами, теряя энергию на выбивание электронов из них и при упругих рассеяниях на их ядрах. Количественной характеристикой слов «почти параллельно» служит т.н. угол Линдхарда, схематически обозначенный желтой прямой — если угол между первоначальным направлением движения иона и осью канала больше чем угол Линдхарда — каналирования нет, если наоборот — ну вы поняли. Заметим, что рисунок сделан с нарушением всех масштабов: на самом деле угол Линдхарда при типичных энергиях ионов очень мал, порядка тысячных долей градуса, что используется в некоторых практических приложениях каналирования и мешает другим.

Основным практическим приложением является контроль качества выращенных монокристаллов — любые дефекты воздействуют на каналирование так же, как перерезание и засорение труб — на работу водопровода. В физике элементарных частиц, на ускорителях, мишени-кристаллы используются для исследования частиц, вылетающих под малым углом к исходному пучку (идущему с ускорителя), обычно такие частицы просто незаметны на фоне пучка, но если кристалл-мишень слегка повернут относительно направления пучка — пучок поглощается, а вторичные частицы каналируются, спокойно вылетают из мишени и регистрируются детектором. Еще одним остроумным приложением на ускорителях является поворот пучков: если кристалл слегка изогнуть, ионы будут двигаться вдоль изогнутых каналов. Для того, чтобы развернуть таким образом пучок протонов энергией 70 ГэВ на 90 градусов достаточно кристалла длиной 75 см (а для того, чтобы сделать это традиционным образом, нужна окруженная сверхмощными магнитами труба длиной где то сто метров). Но как раз тут малость угла Линдхарда сильно мешает, поскольку угловой разброс протонов в пучках в ускорителях гораздо больше чем он. Однако, с увеличением энергии угловой разброс уменьшается, и в ЦЕРНе изогнутый кристалл кремния используется для выведения из ускорителя 450ГеВных протонов (не на коллайдере, долой предрассудки - в ЦЕРНе есть и другие ускорители, кроме Бальшого Агромного).

Различные модели кристаллосгибательных машин

Теперь немного теории. Поскольку ионы движутся быстро (скорость даже низкоэнергических по ядерным масштабам одноМеВных протонов равна 14 тысяч км/сек), атомы с их точки зрения мелькают мимо настолько часто, что сливаются в одно, как доски в заборе с точки зрения едущего мимо лихача. Более строго, длина (вдоль z) одного поперечного колебания зелененькой траектории гораздо больше, чем расстояние между атомами (рисунок и в этом смысле сделан сильно не в масштабе: мне было сложновато изобразить несколько сот атомных слоев, а именно такова «длина волны» одного колебания траектории в реальности) . Благодаря этому, потенциал решетки (который представляет из себя сумму потенциалов ядер и электронных облаков атомов), действующий на ион, можно усреднить вдоль z, в результате остается только зависимость от x, которая выглядит приблизительно так:

Кстати, о траекториях: опять таки из-за того, что ионы тяжелые и энергичные, ихняя длина волны де Бройля (даже поперечная, см. ниже) гораздо меньше, чем ширина канала, поэтому для описания их движения можно использовать обычную классическую механику, и понятие траектории вполне применимо. При движении иона в кристалле выполняется закон сохранения энергии: Кроме того, из за того, что потенциал от z не зависит, сохраняется продольная компонента импульса , и, соответственно, «продольная» часть кинетической энергии , а раз так, то ее можно вычесть из полной энергии и получить поперечную энергию

которая также будет сохранятся. Проведем на графике потенциала пунктирную линию, обозначающую :

Разность по вертикали между пунктирной прямой и красной кривой равна кинетической энергии частицы в данной точке (буде она в ней окажется), а в точках где две линии пересекаются поперечная скорость иона обращается в ноль, это точки где ион отражается от “стенок” канала и идет назад. То есть, если ион при влетании в кристалл оказался во втором от начала отсчета канале, он, если глядеть ему вслед, так и будет мотаться то вправо, то влево между двумя точками поворота. На первом рисунке точки поворота соответствуют максимальным отклонениям зеленой траектории от центра канала.

Теперь рассмотрим случай, когда больше, чем максимумы потенциала
Точек поворота нет, и ион спокойно переходит из канала в канал, на первом рисунке это соответствует красной траектории. То есть, будет ли ион каналирован или нет, зависит от , а она определяется в момент входа в кристалл.

Рассмотрим ион до входа в кристалл. Полная энергия у него та же самая, но она иначе распределена между продольной и поперечной компонентами

где

а - угол между направлением движения иона и формирующими канал атомными цепочками. В момент входа в кристалл продольная кинетическая энергия слегка уменьшается, тратясь на преодоление потенциальной ступеньки

, где - поперечная координата точки входа в кристалл. Поперечная же кинетическая энергия не меняется, значит искомая полная поперечная энергия после входа в кристалл

Последние два утверждения верны постольку поскольку граница кристалла настолько «резкая», что поперечным смещением иона за время прохождения поверхностного слоя кристалла можно пренебречь. Из последней формулы следует, что, будет заканалирован ион или нет, зависит не только от угла, но и от точки входа — если ион влетит в кристалл прямо над центром кристаллической цепочки, то он вообще не может быть каналирован, поскольку его поперечная энергия будет больше максимума потенциала при любом угле. Поэтому более точное определение угла Линдхарта такое: это максимальный угол, при котором каналирование еще возможно, т.е. когда при точке входа совпадающей с минимумом потенциала, что дает формулу для него

Для кремния и протонов  22 эВ. Вывод дан для нерелятивистских ионов, так что для ионов с энергией порядка МеВов полученная формула верна, а для ГеВных — уже нет, так для релятивистских другое соотношение между кинетической энергии и скоростью, вывод для релятивистского случая можно посмотреть тут.

Внимательный читатель может спросить — а почему все время говорится про координаты x и z, и ничего про y? Действительно, для упрощения объяснений я фактически до этого момента говорил только о так называемом плоскостном каналировании, когда каналы формируются между атомными плоскостями (хотя, с бытовой точки зрения каналом это назвать конечно сложно, скорее это похоже на, эээ, ну, ... например, тепловой шов в здании), и вдоль y каналирования нет, ион по этой координате прет по прямой, как и вдоль z. Когда же он удерживается вдоль обоих координат, и действительно идет как по трубе, это называется аксиальным каналированием. Контурная карта потенциала выглядит так

(позаимствовано отсюда), и, соответственно, траектория каналированного иона представляет из себя винтовую линию, наворачивающуюся вокруг точки 0 на картинке.

Даже при движении вдоль канала, ион не может себя чувствовать полностью свободным от общества — он все равно иногда сталкивается с электронами и, если температура кристалла не равно абсолютному нулю, и с тепловыми колебаниями кристаллической решетки. За счет этого он постепенно тормозится, и заодно «забывает» предисторию своего появления в канале — спустя несколько десятков тысяч атомных слоев устанавливается устойчивое распределение плотности пучка ионов в зависимости от расстояния до оси канала. При этом вблизи центра канала плотность пучка максимальна, и в десятки раз превышает плотность пучка до входа в кристалл (если все ионы до входа летели параллельно оси канала, конечно). Еще более радикальное повышение плотности достигается вскоре после входа в канал, в точке, где зелененькая траектория на первом рисунке пересекает центр канала (из за того что вблизи оси канала потенциал зависит от расстояния до оси практически квадратично, частота поперечных колебаний иона не зависит от амплитуды, и все траектории вне зависимости от начального отклонения от оси канала сходятся на оси одновременно), там оно может превышать исходную в сотни раз! Один крупный ученый по этому поводу заимел идею фикс, которую активно пропагандировал: если запускать в тонкую кристаллическую пленку с одной стороны пучок ускоренных ионов дейтерия, а с другой — трития, так чтобы области максимальной плотности встречных пучков совпали, то можно получать энергию за счет ядерной реакции 17.6 МэВ, в обычном ускорителе на встречных пучках такая идея нереализуема вследствие крайней маловероятности столкновения двух ионов из за малой плотности пучков, а увеличение в кристалле плотности пучков в сотни раз увеличит вероятность столкновения в десятки тысяч раз, и не нужно всех этих ваших токамаков. Решив посвятить каналированию один из пунктов заявки на грант, я в качестве оправдания актуальности темы перечислил было и эту замечательную идею. Однако, меня взяли смутные сомнения, которые тут же оправдались: нехитрые оценки с помощью формулы Резерфорда и графика зависимости сечения реакции от энергии дейтрона и тритона показали, что даже для энергии 130кэВ, для которой сечение максимально, сечение деканалирования (в кремнии) вследствие упругого кулоновского рассеяния ионов друг на друге превышает сечение реакции примерно в два миллиона раз... То есть, при столкновении пучков внутри кристалла на одно образования ядра гелия с выходом энергии 17.6 МэВ придется два миллиона деканалированных ионов с полной энергией 260 ГэВ, плотность пучка которых естественно такая же как и без кристалла, так что проблема сведена обратно к обычному столкновению ионов на ускорителе, которое см. выше.