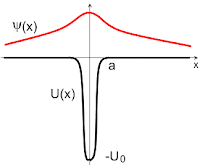
 С одной стороны, известно, что в любом одномерном притягивательном потенциале имеется хотя бы одно связанное состояние. С другой стороны, ясно, что в данном случае это состояние не может поместиться внутрь потенциала, поскольку из-за выписанного выше неравенства кинетическая энергия частицы во много раз превысит потенциальную энергию. Поэтому это состояние будет в основном сидеть в пустом пространстве рядом с потенциалом и только чуть-чуть за него цепляться. Размер локализации частицы будет много больше a, и в первом приближении потенциал будет выглядеть для неё точечным, т.е. потенциалом нулевого радиуса.Потенциалы нулевого радиуса (но с конечным интегралом) обычно описываются с помощью дельта-функций. Поэтому задачу о поиске связанного состояния в короткодействующем потенциале с хорошей точностью можно свести к решению уравнения Шредингера в одномерном дельта-функционном потенциале:
С одной стороны, известно, что в любом одномерном притягивательном потенциале имеется хотя бы одно связанное состояние. С другой стороны, ясно, что в данном случае это состояние не может поместиться внутрь потенциала, поскольку из-за выписанного выше неравенства кинетическая энергия частицы во много раз превысит потенциальную энергию. Поэтому это состояние будет в основном сидеть в пустом пространстве рядом с потенциалом и только чуть-чуть за него цепляться. Размер локализации частицы будет много больше a, и в первом приближении потенциал будет выглядеть для неё точечным, т.е. потенциалом нулевого радиуса.Потенциалы нулевого радиуса (но с конечным интегралом) обычно описываются с помощью дельта-функций. Поэтому задачу о поиске связанного состояния в короткодействующем потенциале с хорошей точностью можно свести к решению уравнения Шредингера в одномерном дельта-функционном потенциале:Другие новости от igorivanov.blogspot.com
Реклама на проекте
Связанное состояние в двумерном точечном потенциале - 1
Saturday, 18 July, 00:07,
igorivanov.blogspot.com
В обычной квантовой механике иногда встречаются задачи, разбираясь с которыми приходится использовать идеи и методы из гораздо более "навороченного" раздела физики -- квантовой теории поля. Сквозь эти, казалось бы совершенно учебные, задачи как бы проглядывает современная физика. Такие задачи можно рекомендовать студентам, которые только-только начали изучать квантовую механику, но уже "рвутся в бой", хотят узнать что-то интересное из более серьезных разделов теорфизики.Одна из таких задач -- поиск связанного состояния в двумерном потенциале нулевого радиуса. В одномерном случае такая задача решается влёт, а в двумерном приводит к совершенно нетривиальным явлениям типа перенормировки и понятию о том, что вообще значит правильно сформулировать задачу. Вообще, это очень известная задача; она изучалась во многих статьях и самыми разными способами. Но поскольку в Рунете про эту задачу, насколько я вижу, ничего нет, то я подумал, что полезно будет в меру понятно и подробно рассказать о ней.Рассказ будет состоять из трех постов: вводная часть, попытка решить задачу в лоб, и переформулировка задачи с ее последующим решением. Это не совсем популярные рассказы, но для студентов-физиков они могут показаться полезными.ВступлениеВ физике встречаются задачи, в которых требуется описать взаимодействие волн вещества (электроны, нейтроны и т.д.) с сильными, но очень короткодействующими потенциалами (радиус действия потенциала много меньше длины волны частиц). Анализ таких задач показывает, что конкретный профиль потенциала тут обычно не существен, а важным является лишь единственное число, характеризуюшее силу потенциала в целом. В этом случае компактный потенциал со сложным профилем можно заменить просто дельта-функцией. Это резко упрощает вычисления при сохранении физической сути явления.В качестве простейшего примера можно взять одномерную квантовомеханическую задачу о поиске связанного состояния в очень короткодействующем притягивательном потенциале с типичной глубиной −U0 и характерным радиусом действия a, для которого выполняется сильное неравенство
 С одной стороны, известно, что в любом одномерном притягивательном потенциале имеется хотя бы одно связанное состояние. С другой стороны, ясно, что в данном случае это состояние не может поместиться внутрь потенциала, поскольку из-за выписанного выше неравенства кинетическая энергия частицы во много раз превысит потенциальную энергию. Поэтому это состояние будет в основном сидеть в пустом пространстве рядом с потенциалом и только чуть-чуть за него цепляться. Размер локализации частицы будет много больше a, и в первом приближении потенциал будет выглядеть для неё точечным, т.е. потенциалом нулевого радиуса.Потенциалы нулевого радиуса (но с конечным интегралом) обычно описываются с помощью дельта-функций. Поэтому задачу о поиске связанного состояния в короткодействующем потенциале с хорошей точностью можно свести к решению уравнения Шредингера в одномерном дельта-функционном потенциале:
С одной стороны, известно, что в любом одномерном притягивательном потенциале имеется хотя бы одно связанное состояние. С другой стороны, ясно, что в данном случае это состояние не может поместиться внутрь потенциала, поскольку из-за выписанного выше неравенства кинетическая энергия частицы во много раз превысит потенциальную энергию. Поэтому это состояние будет в основном сидеть в пустом пространстве рядом с потенциалом и только чуть-чуть за него цепляться. Размер локализации частицы будет много больше a, и в первом приближении потенциал будет выглядеть для неё точечным, т.е. потенциалом нулевого радиуса.Потенциалы нулевого радиуса (но с конечным интегралом) обычно описываются с помощью дельта-функций. Поэтому задачу о поиске связанного состояния в короткодействующем потенциале с хорошей точностью можно свести к решению уравнения Шредингера в одномерном дельта-функционном потенциале:![f?\left[-{\hbar^2\over~2m}{d^2\over~dx^2}+V(x)\right]\psi(x)=E\psi(x)\,,\quad~V(x)=-G\delta(x)\,,](http://dxdt.ru/f?\left[-{\hbar^2\over~2m}{d^2\over~dx^2}+V(x)\right]\psi(x)=E\psi(x)\,,\quad~V(x)=-G\delta(x)\,,) где
где|\approx|U_0|a) . Как изучается буквально на самых первых семинарах по квантовой механике, в таком потенциале существует связанное состояние с энергией
. Как изучается буквально на самых первых семинарах по квантовой механике, в таком потенциале существует связанное состояние с энергией Попытка провести те же самые рассуждения в двумерном случае -- то есть, промоделировать точечный потенциал с помощью двумерной дельта-функции -- неожиданно наталкивается на серьезные трудности. Разбираясь с ними, мы придем к необходимости переформулировать задачу и попутно увидим, как возникают некоторые очень интересные явления, про которые обычно упоминают только в курсах квантовой теории поля.Оценки из соотношения неопределенностейПрежде, чем приступать к честному решению задачи, полезно оценить энергию связанного состояния из соотношения неопределенностей. Вспомним, как это работает в одномерном случае.У нас имеется потенциал с глубиной −U0 и шириной a, причем выполняется выписанное выше неравенство. Пусть Δx -- размер локализации волновой функции. Тогда энергию такого локализованного состояния можно оценить как
Попытка провести те же самые рассуждения в двумерном случае -- то есть, промоделировать точечный потенциал с помощью двумерной дельта-функции -- неожиданно наталкивается на серьезные трудности. Разбираясь с ними, мы придем к необходимости переформулировать задачу и попутно увидим, как возникают некоторые очень интересные явления, про которые обычно упоминают только в курсах квантовой теории поля.Оценки из соотношения неопределенностейПрежде, чем приступать к честному решению задачи, полезно оценить энергию связанного состояния из соотношения неопределенностей. Вспомним, как это работает в одномерном случае.У нас имеется потенциал с глубиной −U0 и шириной a, причем выполняется выписанное выше неравенство. Пусть Δx -- размер локализации волновой функции. Тогда энергию такого локализованного состояния можно оценить как^2}\,-\,U_0{a\over\Delta~x}\,.) Для потенциальной энергии мы учли, что потенциал "ощущается" не всей волновой функцией, а только малой ее частью в области действия потенциала. Эта энергия имеет минимум при
Для потенциальной энергии мы учли, что потенциал "ощущается" не всей волновой функцией, а только малой ее частью в области действия потенциала. Эта энергия имеет минимум при  , и равна она
, и равна она  Из-за неравенства получается, что
Из-за неравенства получается, что  , т.е. уровень получается очень мелкий.Попробуем записать то же в двумерном случае для потенциала глубиной −U0 и областью действия a в обоих направлениях.
, т.е. уровень получается очень мелкий.Попробуем записать то же в двумерном случае для потенциала глубиной −U0 и областью действия a в обоих направлениях.^2}\,-\,U_0{a^2\over(\Delta x)^2}\,.) Зависимость от Δx в кинетическом и потенциальном слагаемых получилась одинаковой. Это значит, что нам не удастся минимизировать потенциал ни при каких конечных Δx. То есть, с помощью такой оценки не удается "разглядеть", существует ли в таком потенциале связанное состояние или нет. (Более аккуратный подход показывает, что связанное состояние всегда есть, но с экспоненциально малой энергией связи.)Итак, уже простые оценки показывают, что в случае двумерного потенциала нулевого радиуса нас ожидают какие-то сюрпризы. В следующем посте мы попробуем решить эту задачу честно и увидим, на каком именно этапе у нас возникают проблемы.
Зависимость от Δx в кинетическом и потенциальном слагаемых получилась одинаковой. Это значит, что нам не удастся минимизировать потенциал ни при каких конечных Δx. То есть, с помощью такой оценки не удается "разглядеть", существует ли в таком потенциале связанное состояние или нет. (Более аккуратный подход показывает, что связанное состояние всегда есть, но с экспоненциально малой энергией связи.)Итак, уже простые оценки показывают, что в случае двумерного потенциала нулевого радиуса нас ожидают какие-то сюрпризы. В следующем посте мы попробуем решить эту задачу честно и увидим, на каком именно этапе у нас возникают проблемы.
 С одной стороны, известно, что в любом одномерном притягивательном потенциале имеется хотя бы одно связанное состояние. С другой стороны, ясно, что в данном случае это состояние не может поместиться внутрь потенциала, поскольку из-за выписанного выше неравенства кинетическая энергия частицы во много раз превысит потенциальную энергию. Поэтому это состояние будет в основном сидеть в пустом пространстве рядом с потенциалом и только чуть-чуть за него цепляться. Размер локализации частицы будет много больше a, и в первом приближении потенциал будет выглядеть для неё точечным, т.е. потенциалом нулевого радиуса.Потенциалы нулевого радиуса (но с конечным интегралом) обычно описываются с помощью дельта-функций. Поэтому задачу о поиске связанного состояния в короткодействующем потенциале с хорошей точностью можно свести к решению уравнения Шредингера в одномерном дельта-функционном потенциале:
С одной стороны, известно, что в любом одномерном притягивательном потенциале имеется хотя бы одно связанное состояние. С другой стороны, ясно, что в данном случае это состояние не может поместиться внутрь потенциала, поскольку из-за выписанного выше неравенства кинетическая энергия частицы во много раз превысит потенциальную энергию. Поэтому это состояние будет в основном сидеть в пустом пространстве рядом с потенциалом и только чуть-чуть за него цепляться. Размер локализации частицы будет много больше a, и в первом приближении потенциал будет выглядеть для неё точечным, т.е. потенциалом нулевого радиуса.Потенциалы нулевого радиуса (но с конечным интегралом) обычно описываются с помощью дельта-функций. Поэтому задачу о поиске связанного состояния в короткодействующем потенциале с хорошей точностью можно свести к решению уравнения Шредингера в одномерном дельта-функционном потенциале:




Комментарии (0)